【新智元导读】本文提出了SAX-NeRF框架,一种专为稀疏视角下X光三维重建设计的新型NeRF方法,通过Lineformer Transformer和MLG采样策略显著提升了新视角合成和CT重建的性能。研究者还建立了X3D数据集,并开源了代码和预训练模型,为X光三维重建领域的研究提供了宝贵的资源和工具。
众所周知,X 光由于有着十分强大的穿透力而被广泛地应用于医疗、安检、考古、生物、工业检测等场景的透射成像。
然而,X 光的辐射作用对人体是有害的,受试者与测试者都会或多或少地收到影响。为了减少 X 光对人体的伤害,人们开始研究稀疏视角下的 X 光重建从而降低在 X 光中的暴露时间。
这主要包含了两个子任务:
1. 新视角合成,即从一个被扫描物体的一些已拍摄的视角来合成出新的没有被拍摄过的视角下该物体的投影。
2. CT 重建,即从多视角的 X 光投影中恢复出密集的三维 CT 体辐射密度 (volume radiodensity)。
辐射密度刻画的是当 X 光穿透物体时,X 光被吸收或者阻挡的程度大小。如图 2 所示,自然光成像主要靠的是光线在物体表面的反射。
而 X 光成像主要依靠的是 X 光穿透物体后被吸收或阻挡。换句话说,自然光成像关注并捕获的是物体表面的信息如纹理颜色等,而 X 光成像关注的更多的是物体内部的结构和材质。
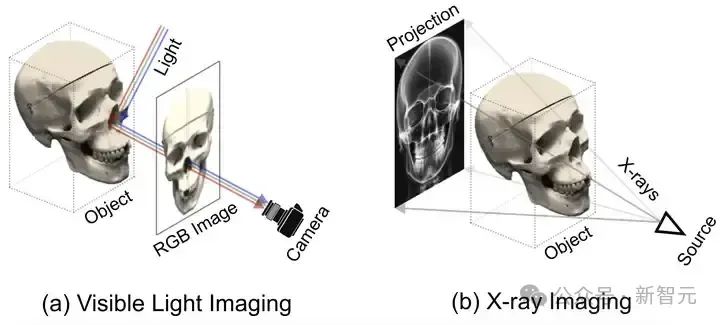
图1 自然光成像原理对比 X 光成像原理
也正是因为自然光成像和 X 光成像之间的显著差异,自然光下的 NeRF 方法以及对应的公式并不适用于 X 光。
针对 X 光的三维重建问题,本文提出了一种用于稀疏视角下 X 光三维重建的 NeRF 方法。具体而言,主要做两个任务。一是 X 光的新视角合成 (Novel View Synthesis, NVS),二是 CT 重建,可以简单理解为体密度的重建。

论文链接: https://arxiv.org/abs/2311.10959
代码链接: https://github.com/caiyuanhao1998/SAX-NeRF
演示视频:https://www.youtube.com/watch?v=oVVUaBY61eo
leaderboard: https://paperswithcode.com/dataset/x3d

X 光三维重建动态 demo
先给大家看一个在新视角合成任务上的性能对比图:
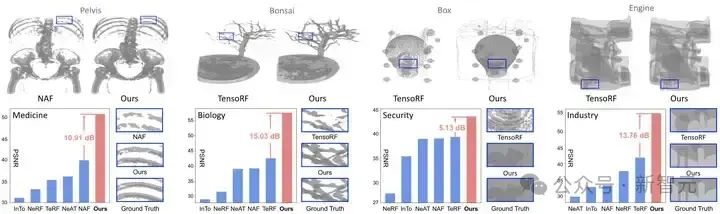
图2 我们的方法与 SOTA 方法在医学、生物、安检、工业场景上的新视角合成性能对比
目前所有的训练测试代码、预训练权重、训练日志、数据、测试结果均已开源。此外,我们已经在 paper with code 设置好了 leaderboard, 欢迎大家来提交结果。
我们将开源的 github repo 拓展成了一个支持 9 类算法的工具包方便大家的科研工作。除此之外,我还把数据可视化的代码,和造数据的代码也一起公开了,以方便有条件的可以接触到CT数据的朋友可以在自己搜集的数据上开展研究。
文中主要做出了以下四点贡献:
1. 提出了一套全新的能够同时做 X 光新视角合成与 CT 成像的 NeRF 框架,名为 SAX-NeRF。该框架的训练不需要用的 CT 作为监督信号,只使用 X 光片即可。
2. 设计了一种新的分段式 Transformer,名为 Lineformer,可以捕获成像物体在三维空间中的复杂的内部结构。据我们所知,我们的 Lineformer 是首个将 Transformer 应用于 X 光渲染的 Transformer。
3. 提出了一种新型的射线采样策略,名为 MLG sampling,可以从 X 光片上提取出局部和全局的信息。
4. 搜集了首个大规模的 X 光三维重建数据集,涵盖医疗、生物、安检、工业领域。同时,我们设计的算法在这个数据集上取得了当前最好效果,在 X 光新视角合成和 CT 重建两大任务上比之前的最好方法要高出 12.56 和 2.49 dB。
空间坐标系的转换
我们在圆形扫描轨迹锥形 X 光束扫描(circular cone-beam X-ray scanning)场景下研究三维重建问题。空间坐标系的变换关系如图 3 所示。
被扫描物体的中心 O 为世界坐标系的原点。扫描仪的中心 S 为相机坐标系的中心。探测器 D 的左上角为图像坐标系的原点。整个空间坐标系的变换遵循 OpenCV 三维视觉的标准。
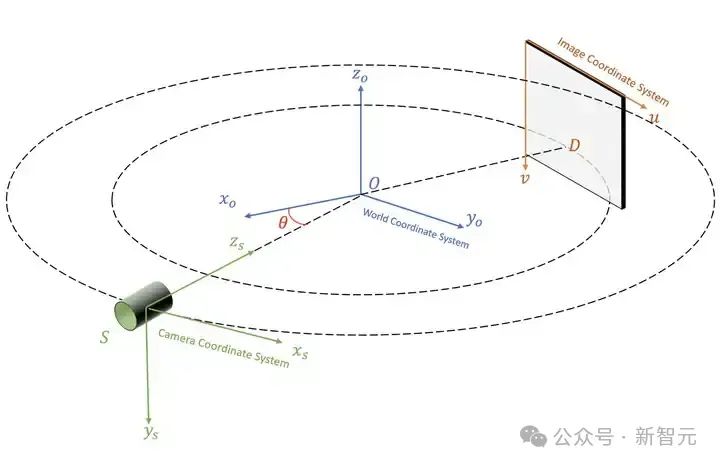
图3 空间坐标系转换关系示意图
本文方法
NeRF 从自然光成像到 X 光成像
在自然光成像中,NeRF采用一个 MLP Θ 来拟合的是空间中点的位置 (��,��,��) 和视角 (��,��) 到该点的颜色 (��,��,��) 和体密度 (��) 的隐式映射:
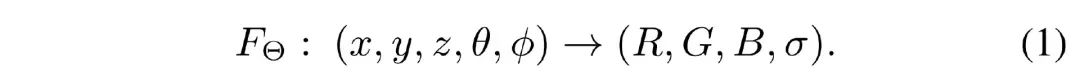
而在 X 光成像中,并不关注颜色信息,只需要重建出辐射密度 ��。
同时我们注意到辐射密度属性与观测的视角无关。因此,我们指出,X 光下的 NeRF 公式应当为:
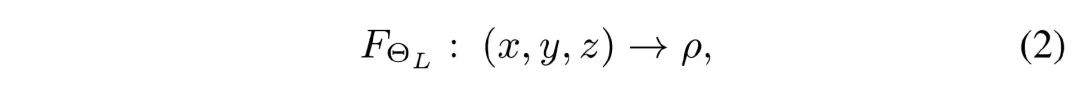
其中的 Θ�� 表示我们 Lineformer 的可学习参数。根据 Beer-Lambert 规则,一条 X 光射线的强度会沿着它所穿过的物体的辐射密度的积分而呈指数型衰减。如下公式所示:
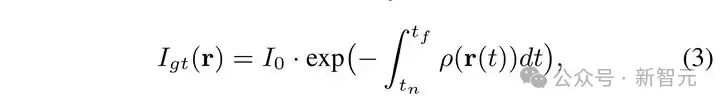
将公式 (3)中的积分离散化,同时将其中的 ��(��(��)) 用我们 Lineformer 预测的 ���� 替代便可得到预测的 X 光强度,如公式(4)所示:
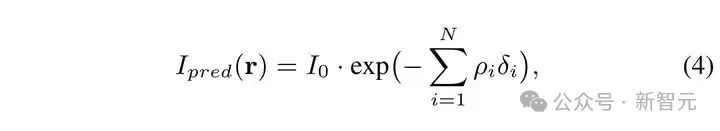
我们的训练监督目标是预测的 X 光强度与真实的 X 光强度之间的均方误差:
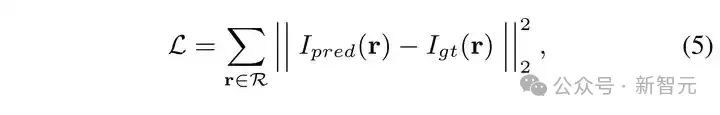
Lineformer — 分段式 Transformer
我们注意到 X 光的成像过程是沿着穿透物体被吸收或者阻挡,成像物体不同部分的结构和材质存在差异,因此 X 光被吸收的程度也不一致。
然而之前的 NeRF 类方法大都使用很常规的 MLP 网络平等地对待沿着射线上的采样点。如果直接采用 MLP 来拟合公式(3)的话,那 X 光成像的重要性质便被忽略了,难以取得很好的效果。
基于此,我们提出了一种新型的分段式 Transformer (Line Segment-based Transformer,简称 Lineformer)来拟合 X 光在穿透不同结构时的衰减。
我们的算法框架如图 4 所示。我们首先采用 MLP sampling 策略采样出一个 batch 的 X 光射线 �� 。
对每一条射线,我们采出一组三维点的位置 �� 。将 �� 通过一个哈希编码器 �� 得到点特征 ��。然后 �� 经过 4 个分段式注意力块(Line Segment-based Attention Block,简称为 LSAB)与两层全连接层便可得到这些点的辐射密度 ��
。
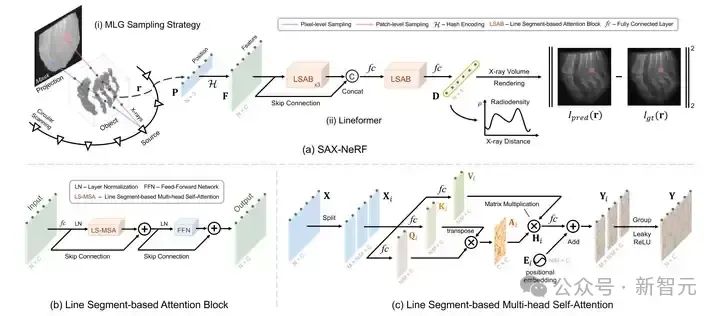
图4 SAX-NeRF 的算法框架图
LSAB 中最核心的模块是分段式的多头自注意力机制(Line Segment-based Multi-head Self-Attention,LS-MSA),其结构如图 4 (c)所示。将输入的点特征记为 ��∈����×�� ,将其分为 M 段:
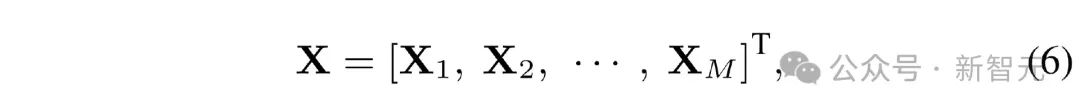
其中的 ����∈������×�� 。然后 ���� 会被线性地投影到 ���� 、���� 、���� :
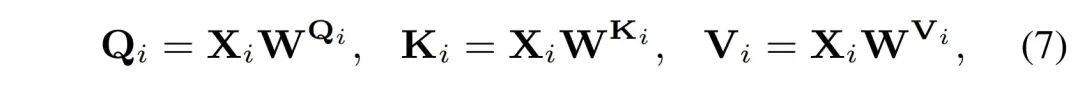
然后将 ���� 、 ���� 、 ���� 沿着通道维度均匀地分成 k 个头:
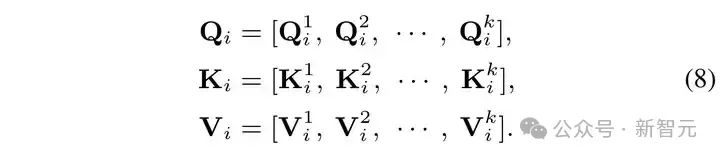
然后在每一个头内计算自相似注意力 ������ 如下:
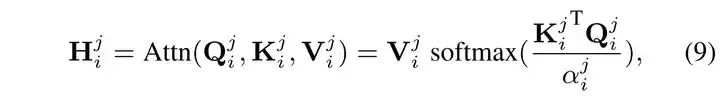
然后将计算结果拼接起来,通过一个全连接层后与一个位置编码 ���� 相加后得到一段的输出:

将 M 段输出拼接起来便得到总的输出:
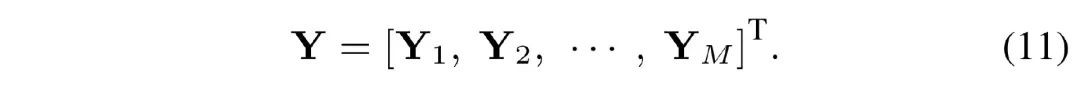
分析我们的 LS-MSA 计算复杂度如下:
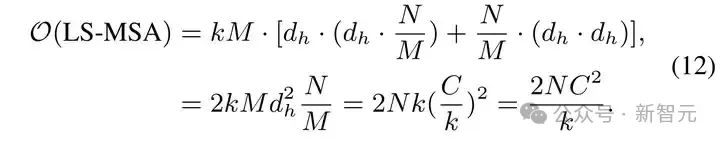
与采样的点数 �� 呈线性相关。对比全局多头自注意力机制的计算复杂度:
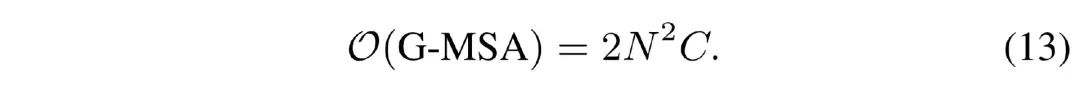
与采样的点数 �� 呈二次相关。因此我们的方法计算量比常规的 Transformer 要小得多。
X 射线采样策略
由于 RGB 成像中信息普遍比较密集,即一张 RGB 图像中几乎每一个像素都传递信息。因此,RGB NeRF 在采射线时通常会使用随机的方式在图像上采集一批像素点,如图5 (a) 中的蓝色像素所示,每一个像素点对应一条射线。
然而这种射线采样的策略并不适用于 X 光图片,因为 X 光片有着较大的空间稀疏性。如果随机采样的话,可能有一些采样点不落在成像区域,如图 5 (a) 中的像素点 ������ 。为了解决这个问题,我们设计了一种高效的射线
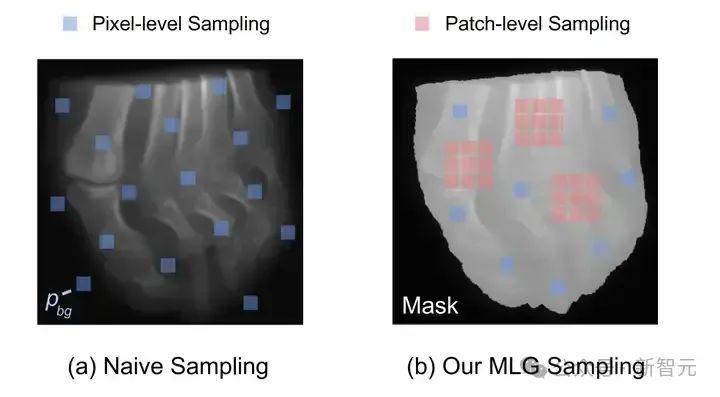
图5 简单随机采样 (a) 与我们的采样策略 (b) 的对比
采样策略,名为 MLG sampling,如图 (b) 所示。首先,我们用一个二值化的掩膜将成像区域分割出来。然后我们将整个图像分成互不重叠的小方块。
然后我们随机抽选 M 个完全落在成像区域的小方块,取出小方块内所有的像素对应的射线。在成像区域的其他位置(除开被选取的小方块外),我们还再继续抽取 N 个像素点对应的射线。
将两次抽取的射线组成一个 ray batch 用作训练。如此采样得到的射线首先全都穿透被扫描物体,捕获到被扫描物体的辐射密度信息。同时成块的区域还有着丰富的语义上下文信息以帮助三维重建。
实验结果
新视角合成
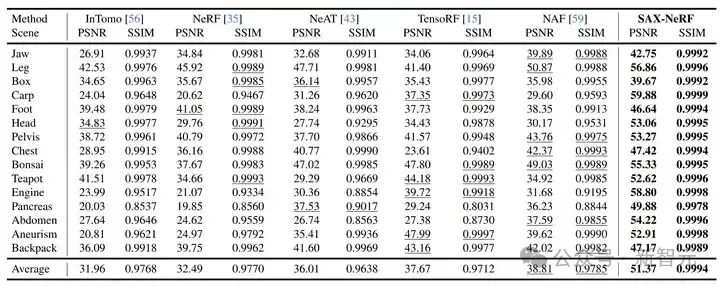
表1 新视角合成的定量实验结果对比
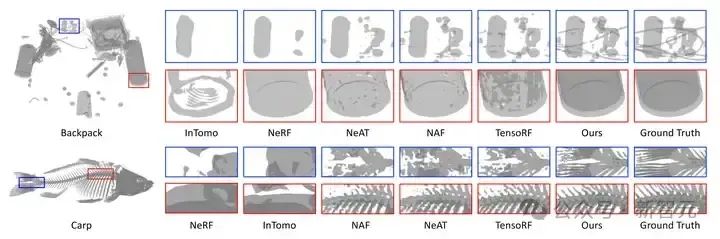
图6 新视角合成的视觉结果对比
新视角合成任务上的定量指标和视觉对比分别如表 1 和图 6 所示。我们的方法比之前最好方法还要高出 12.56 dB。
CT 图像重建
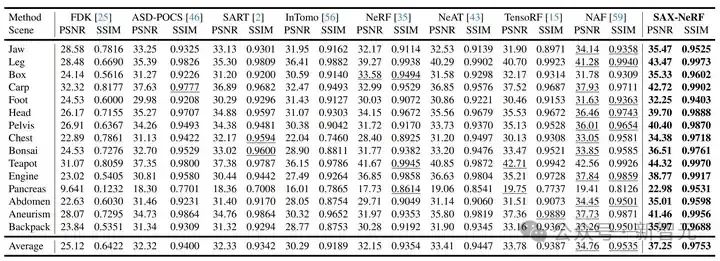
表2 CT 图像重建定量指标对比

图7 CT 图像重建的视觉对比
CT 图像重建的定量指标和视觉对比分别如表 2 与图 7 所示。我们的方法比之前最好的方法要高出 2.5 dB。
总结与后记
本文针对 X 光三维重建问题,设计了一套基于 NeRF 的可同时进行 X 光新视角合成与 CT 重建的算法框架 SAX-NeRF。搜集了一个大规模的 X 光三维重建数据集 X3D。
目前我已经将开源的 github repo 做成了一套相对完善的 codebase,支持 9 类算法,包含了数据生成、可视化的辅助功能函数代码。
参考资料:
https://arxiv.org/abs/2311.10959